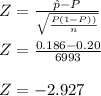Question

When testing gas pumps for accuracy, fuel-quality enforcement specialists tested pumps andfound that 1304 of them were not pumping accurately (within 3.3 oz when 5 gal ispumped),and 5689 pumps were accurate. Use a 0.01 significance level to test the claimof an industryrepresentative that less than 20% of the pumps are inaccurate.

Answer 1

The p-value of the test statistic from the standard normal table is 0.0017 which is less than the level of significance therefore, the null hypothesis would be rejected and it can be concluded that there is sufficient evidence to support the claim that less than 20% of the pumps are inaccurate.

Explanation:

Here, 1304 gas pumps were not pumping accurately and 5689 pumps were accurate.

x = 1304, n = 1304 + 5689 = 6993

The level of significance = 0.01

The sample proportion of pump which is not pumping accurately can be calculated as,

The claim is that the industry representative less than 20% of the pumps are inaccurate.

The hypothesis can be constructed as:

H0: p = 0.20

H1: p < 0.20

The one-sample proportion Z test will be used.

The test statistic value can be obtained as:

`Z=\frac{\hat{p}-P}{\sqrt{(P(1-P)))/(n)}}\\\\Z=(0.186-0.20)/(6993)\\\\Z=-2.927`