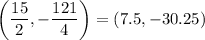Question

The quadratic function y = x² - 15x + 26 is drawn below. Use the symmetry of the quadratic curve to find the coordinates of the minimum.​

Answer 1

`\left((15)/(2),-(121)/(4)\right)=(7.5,-30.25)`

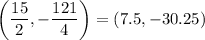
Explanation:

The given graph shows the graph of the quadratic function y = x² - 15x + 26, which is a parabola that opens upwards.

The minimum point of an upwards opening parabola is its vertex.

The axis of symmetry of a quadratic function is the vertical line that passes through the vertex, dividing the parabola into two symmetrical halves.

The axis of symmetry is the x-coordinate of the vertex and is always equidistant from the two x-intercepts. Therefore, to find the x-coordinate of the vertex, find the x-value of the midpoint of the x-intercepts:

`\textsf{$x$-coordinate of the vertex}=(2+13)/(2)=(15)/(2)`

To find the y-coordinate of the vertex, substitute the x-coordinate into the given function:

`\begin{aligned}x=(15)/(2) \implies y&=\left((15)/(2)\right)^2-15\left((15)/(2)\right)+26\\\\y&=(225)/(4)-(225)/(2)+26\\\\y&=-(121)/(4)\\\\y&=-30.25\end{aligned}`

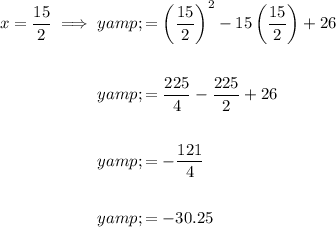
Therefore, the coordinates of the minimum point of the given quadratic function are:

`\left((15)/(2),-(121)/(4)\right)=(7.5,-30.25)`