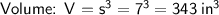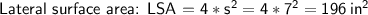Question

!50 POINTS! (3 SIMPLE GEOMETRY QUESTIONS)

QUESTIONS BELOW
|
|
\/

Answer 1

For 1st question:

`\tt V = \boxed{ 576} cm^3`

`\tt LA = \boxed{ 288} cm^2`

`\tt SA = \boxed{ 432 } cm^2`

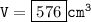
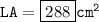
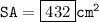
For 2nd question:

`\tt V = \boxed{ 768 \pi} cm^3`

`\tt LA = \boxed{ 192 \pi } cm^2`

`\tt SA = \boxed{ 320 \pi } cm^2`

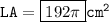
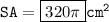
For 3rd question:

`\tt V = \boxed{ 343} in^3`

`\tt LA = \boxed{ 196} in^2`

`\tt SA = \boxed{ 294} in^2`

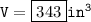
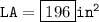
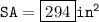
Explanation:

For 1st Question:

The figure is cuboid.

A cuboid is a three-dimensional shape with six rectangular faces.

• The volume of a cuboid is the length * width * height.
• The lateral surface area is the area of the faces that are parallel to the height.
• The total surface area is the sum of the areas of all six faces.

In this case:

• length(l) = 12 cm
• Width(w) = 6 cm
• height(h) = 8 cm

Now, substituting value in above formula, let's calculate.

`\sf \textsf{Volume: V = l * w * h =} 12*6*8 = 576 cm^3`

`\sf \textsf{ Lateral surface area: LSA = 2 * (l + w) * h =} 2*(12+6)*8 = 288 cm^2`

`\sf \textsf{Total surface area: TSA = 2 * (lw + lh + wh) = }2(12*6+12*8+6*8) = 432 cm^2`

`\hrulefill`

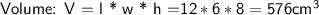
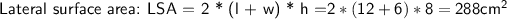
For 2nd Question:

The figure is cylinder.

A cylinder is a three-dimensional shape with two circular bases and a curved surface that is parallel to the bases.

• The volume of a cylinder is the area of the base * height.
• The lateral surface area is the area of the curved surface.
• The total surface area is the sum of the areas of the two bases and the curved surface.

In this case:

• radius(r) = 8 cm
• height(h) = 12 cm

Now, substituting value in above formula, let's calculate.

`\sf \textsf{Volume: V = } \pi* r^2 * h= \pi * 8^2 * 12 =768 \pi \:cm^3`

`\sf \textsf{ Lateral surface area: LSA =} 2 * \pi*8 * 12 = 192 \pi \:cm^2`

`\sf \textsf{Total surface area:TSA = }2 * \pi * r(r +h) = 2 \pi * 8(8+12) =320 \pi \: cm^2`

`\hrulefill`

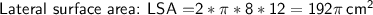
For 3rd Question:

The figure is cube.

A cube is a three-dimensional shape with six square faces.

• The volume of a cube is the side length * side length * side length.
• The lateral surface area is the area of the faces that are parallel to the height.
• The total surface area is the sum of the areas of all six faces.

In this case:

• length(s) = 7 in

Now, substituting value in above formula, let's calculate.

`\sf \textsf{Volume: V = }s^3 = 7^3 = 343 \: in^3`

`\sf \textsf{Lateral surface area: LSA = }4 * s^2 =4* 7^2 = 196 \: in^2`

`\sf \textsf{Total surface area: TSA = }6 * s^2 = 6*7^2= 294 \: in^2`