Question

Please solve thank you so much

Answer 1

2√5 units ≈ 4.47 units (nearest hundredth)

Explanation:

To find the distance between point A and O(0, 0), we first need to find the coordinates of point A.

Given linear equations:

`\begin{cases}y=x-6\\y=-(1)/(2)x\end{cases}`

We are told that point A is the point of intersection of the two lines.

Therefore, to find the x-coordinate of point A, substitute the first equation into the second equation and solve for x:

`\begin{aligned}x-6&=-(1)/(2)x\\\\(x-6) \cdot 2&=-(1)/(2)x \cdot 2\\\\2x-12&=-x\\\\2x-12+x&=-x+x\\\\3x-12&=0\\\\3x-12+12&=0+12\\\\3x&=12\\\\(3x)/(3)&=(12)/(3)\\\\x&=4\end{aligned}`

Substitute the found value of x into the first equation and solve for y:

`\begin{aligned}y&=4-6\\\\y&=-2\end{aligned}`

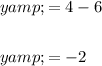
Therefore, the coordinates of A are (4, -2).

To find the distance between A(4, -2) and O(0, 0) we can use the distance formula.

`\boxed{\begin{minipage}{7.4 cm}\underline{Distance Formula}\\\\$d=√((x_2-x_1)^2+(y_2-y_1)^2)$\\\\\\where:\\ \phantom{ww}$\bullet$ $d$ is the distance between two points. \\\phantom{ww}$\bullet$ $(x_1,y_1)$ and $(x_2,y_2)$ are the two points.\\\end{minipage}}`

Substitute the two points into the formula and solve for d:

`\begin{aligned}d&=√((x_O-x_A)^2+(y_O-y_A)^2)\\&=√((0-4)^2+(0-(-2))^2)\\&=√((-4)^2+(2)^2)\\&=√(16+4)\\&=√(20)\\&=√(2^2\cdot 5)\\&=√(2^2)√(5)\\&=2√(5)\end{aligned}`

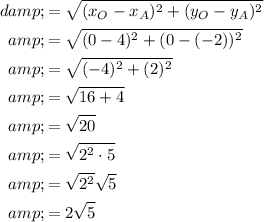
Therefore, the distance between point A and O(0, 0) is 2√5 units, which is approximately 4.47 units (rounded to the nearest hundredth).