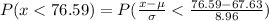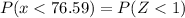Answer:
(a)P(x>85.55)=0.02275
(b)

Explanation:
We are given that
Average sales for an online textbook distributor per customer per purchase
,
 $67.63
$67.63
Standard deviation of the amount spent on textbooks,
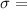 $8.96
$8.96
(a) We have to find probability for a randomly selected customer spent more than $85.55 per purchase.
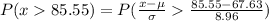
=

=
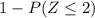
=

P(x>85.55)=0.02275
(b)We have to find probability for a randomly selected customer spent less than $76.59 per purchase