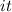Answer:
Using the trigonometric identity for the cosine of the sum of two angles, we have:
cos(a + b) = cos(a)cos(b) - sin(a)sin(b)
cos(a - b) = cos(a)cos(b) + sin(a)sin(b)
Substituting a = π/4 and b = x, we get:
cos(π/4 + x) = cos(π/4)cos(x) - sin(π/4)sin(x) = (1/√2)cos(x) - (1/√2)sin(x)
cos(π/4 - x) = cos(π/4)cos(x) + sin(π/4)sin(x) = (1/√2)cos(x) + (1/√2)sin(x)
Adding the two equations, we get:
cos(π/4 + x) + cos(π/4 - x) = (1/√2)cos(x) - (1/√2)sin(x) + (1/√2)cos(x) + (1/√2)sin(x)
Simplifying, we get:
cos(π/4 + x) + cos(π/4 - x) = (√2/2)cos(x) + (√2/2)sin(x)
Therefore,
cos(π/4 + x) + cos(π/4 - x) = (√2/2)cos(x) + (√2/2)sin(x)