Question

You measure 25 turtles' weights, and find they have a mean weight of 31 ounces. Assume the population standard deviation is 12.8 ounces. Based on this, what is the maximal margin of error associated with a 90% confidence interval for the true population mean turtle weight. Give your answer as a decimal, to two places

Answer 1

Margin of error = 4.21 ounces

Explanation:

According to the Question,

• Given That, You measure 25 turtles' weights, and find they have a mean weight of 31 ounces. Assume the population standard deviation is 12.8 ounces

Therefore, Sample mean = 31 ounces , Sample size(n) = 25 , Alpha(α) = 0.10 & Population standard deviation(σ) = 12.8 ounces

• Thus, Margin of error =
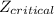  `Z_(critical)` × σ / √n (
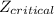  `Z_(critical)` at α=.010 is 1.645)

Putting The Values, We get

1.645 × (12.8 / √25 ) ⇒ 4.2112 ≈ 4.21

Thus, the maximum margin of error associated with a 90% confidence interval for the true population mean turtle weight is 4.21 ounces