Question

Prove that tan theta * sin theta = (1 - cos^2 theta)/(sqrt(1 - sin^2 theta))​

Answer 1

This identity holds as long as
`\displaystyle \theta \\e k\, \pi + (\pi)/(2)` for all integer
`k`.

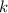For the proof, make use of the fact that:

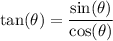`\displaystyle \tan(\theta) = (\sin(\theta))/(\cos(\theta))` (definition of tangents,) and

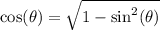`\cos(\theta) = \sqrt{1 - \sin^(2)(\theta)}` (Pythagorean identity,) which is equivalent to
`1 - \cos^(2)(\theta) = \sin^(2)(\theta)`.

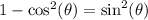Explanation:

Assume that
`\displaystyle \theta \\e k\, \pi + (\pi)/(2)` for all integer
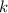`k`. This requirement ensures that the
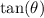`\tan(\theta)` on the left-hand side takes a finite value. Doing so also ensures that the denominator
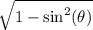`√(1 - \sin^2(\theta))` on the right-hand side is non-zero.

Make use of the fact that
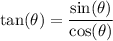`\displaystyle \tan(\theta) = (\sin(\theta))/(\cos(\theta))` to rewrite the left-hand side:

`\begin{aligned} & \tan(\theta) \cdot \sin(\theta) \\ =&\; \frac{\sin({\theta})}{\cos({\theta})} \cdot \sin(\theta) \\ =&\; (\sin^(2)(\theta))/(\cos(\theta))\end{aligned}`.

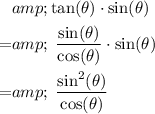Apply the Pythagorean identity
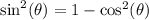`\sin^(2)(\theta) = 1 - \cos^(2)(\theta)` and
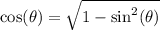`\cos(\theta) = \sqrt{1 - \sin^(2)(\theta)}` to rewrite this fraction:

`\begin{aligned} & (\sin^(2)(\theta))/(\cos(\theta))\\ =\; &(1 - \cos^(2)(\theta))/(\cos(\theta))\\ =\; & \frac{1 - \cos^(2)(\theta)}{\sqrt{1 - \sin^(2)(\theta)}}\end{aligned}`.

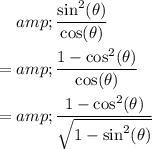Hence,
`\displaystyle \tan(\theta) \cdot \sin(\theta) = \frac{1 - \cos^(2)(\theta)}{\sqrt{1 - \sin^(2)(\theta)}}`.