Question

Algebra 2 question pls answer fast

Answer 1

a)

`( (h)/(g) )(x) = (h(x))/(g(x)) = \frac{ - 7 + 3 {x}^(2) }{7 - 3x}`

`( (h)/(g)) (4) = (h(4))/(g(4)) = \frac{ - 7 + 3( {4}^(2)) }{7 - 3(4)} =`

`( - 7 + 3(16))/(7 - 12) = ( - 7 + 48)/( - 5) = - (41)/(5) = - 8.2`

b) 7 - 3x ≠ 0, so x ≠ 7/3.

7/3 (2 1/3) is not in the domain of h/g.

Answer 2

`\textsf{(a)}\quad \left((h)/(g)\right)(4)=\boxed{-(41)/(5)}`

`\textsf{(b)}\quad \textsf{Value(s) that are NOT in the domain of $(h)/(g)$\;:}\;\;\boxed{(7)/(3)}`

Explanation:

Given functions:

`\begin{cases}h(x)=-7+3x^2\\g(x)=7-3x\end{cases}`

`\hrulefill`

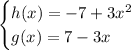
Part (a)

To find the value of (h/g)(4), we need to evaluate the function h(x) divided by g(x) at x = 4.

`\begin{aligned}\left((h)/(g)\right)(4)&=(h(4))/(g(4))\\\\&=(-7+3(4)^2)/(7-3(4))\\\\&=(-7+3(16))/(7-3(4))\\\\&=(-7+48)/(7-12)\\\\&=(41)/(-5)\\\\&=-(41)/(5)\end{aligned}`

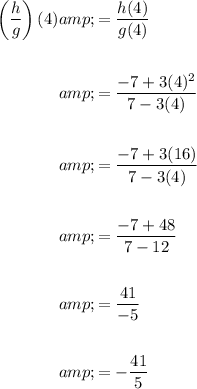
Therefore, (h/g)(4) is equal to -41/5.

`\hrulefill`

Part (b)

To find the values of x that are not in the domain of (h/g), we need to consider the restrictions imposed by the division operation.

The division (h/g) is undefined when the denominator g(x) equals zero. Therefore, we must exclude any x-values that would make the denominator zero.

Set g(x) to zero and solve for x:

`\begin{aligned}g(x)&=0\\\\\implies 7-3x&=0\\\\7&=3x\\\\3x&=7\\\\x&=(7)/(3)\end{aligned}`

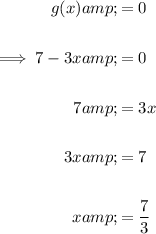
Therefore, x = 7/3 is not in the domain of (h/g).