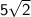Question

Helppp pleaseeeeeeeeeee

Answer 1

Here trigonometric ratio will be used.

As we can see the figure where 5 is the perpendicular and we have to calculate the value of x.

x is Hypotenuse

Using trigonometric ratio:

`\sf \: (P)/(H) = \sin \theta`

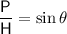
Where P is perpendicular and H is Hypotenuse.

Since hypotenuse is x and the value of perpendicular is 5. Therefore by substituting the values of Perpendicular and Hypotenuse in the above trigonometric ratio we will get required value of x.

Also, The value of
`\theta` will be 45°

`\sf(5)/(x) = \sin 45\degree`

`\sf(5)/(x) = (1)/( √(2) ) \: \: \: \: \: \: \: \: \: \: \: \bigg( \because \sin45 \degree = (1)/( √(2) ) \bigg)`

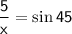
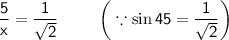
Further solving by cross multiplication,

`\sf x = 5 √(2)`

So the value of x is
`\sf 5 √(2)`