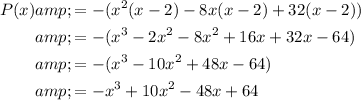Answer:
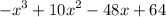
Explanation:
We want to find the minimum-degree polynomial with real coefficients and zeros at:
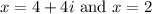
As well as a y-intercept of 64.
By the Complex Root Theorem, if a + bi is a root, then a - bi is also a root.
So, a third root will be 4 - 4i.
The factored form of a polynomial is given by:
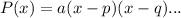
Where a is the leading coefficient and p and q are the zeros. More factors can be added if necessary.
Substitute:
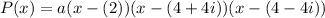
Since we want the minimum degree, we won't need to add any exponents.
Expand the second and third factors:
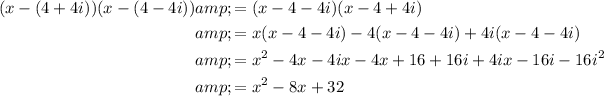
Hence:
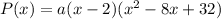
Lastly, we need to determine a. Since the y-intercept is y = 64, this means that when x = 0, y = 64. Thus:
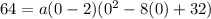
Solve for a:
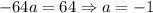
Our factored polynomial is:
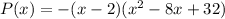
Finally, expand: