Question

The diameter of Jacob's circular tabletop is 6 feet. What is the area, in square feet, of Jacob's tabletop?

Answer 1

The area is:

28.27 square feet

Work/explanation:

Since the tabletop is circular, we use the formula for a circle's area, which is:
`\bf{A=\pi r^2}`.

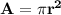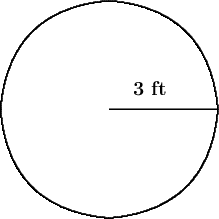
We have the diameter, and to find the radius, we divide the diameter by 2, which gives us 6 ÷ 2 = 3 feet, so the radius of the tabletop is 3 feet.

Now, here's a diagram for you;

`\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\qbezier(2.3,0)(2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,-2.121)(0,-2.3)\qbezier(2.3,0)(2.121,-2.121)(-0,-2.3)\put(0,0){\line(1,0){2.3}}\put(0.5,0.3){\bf\large 3\ ft}\end{picture}`

Plug in the data:

`\sf{A=\pi*3^2}`

`\sf{A=\pi*9}`

`\sf{A=28.27\:ft^2}`

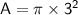
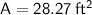
Hence, the area is 28.27 square feet.

Answer 2

approximately 28.26 square feet

Explanation:

The formula for the area of a circle is A = pi(r)^2. So, the radius is half of the diameter, meaning it's 3 feet. Then we square it to get 9, and multiply by pi, or 3.14. This leads us to the approximated answer of 28.26 square feet.