Question

8. The first three terms of a geometric sequence are ( x-6), 3x, and y. If the common ratio is 6, then the value of y is.

Answer 1

The value of y is 216

(and the value of x is 12)

Explanation:

The general formula for a geometric sequence is,

`a_n = a_1(r)^(n-1)`

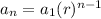
Where n represents the nth term, a_1 is the first term and r is the common ratio,

we see that,

r = 6,

the first term is,

a_1 = (x-6)

the 2nd term is,

a_2 = 3x,

the 3rd term is,

a_3 = y, finding y,

first we find x, using the above given formula we have,

`a_2 = a_1(6)^(2-1)\\3x = (x-6)(6^1)\\3x = 6x -36\\36 = 6x - 3x\\36 = 3x\\x=36/3\\x=12`

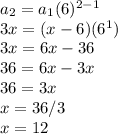
x = 12,

Now, for y we can use the relation between a_3 and a_2,

`a_3 = a_1(6)^(3-1)\\y = (x-6)(6)^2\\y = (12-6)(6^2)\\y = 6(6^2)\\y = 6^3\\y = 216`

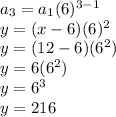
y = 216