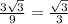Question

Need help pls fast bro

Answer 1

`\sin \theta =(1)/(2)`

`\cos \theta=(√(3))/(2)`

`\tan \theta=(√(3))/(3)`

Explanation:

The given diagram shows a right triangle with an interior angle marked θ.

• The side opposite angle θ is labelled 3√3.
• The side adjacent angle θ is labelled 9.
• The hypotenuse of the triangle is labelled 6√3.

To find the sine, cosine, and tangent of θ, use the trigonometric ratios.

`\boxed{\begin{minipage}{9.4 cm}\underline{Trigonometric ratios} \\\\$\sf \sin(\theta)=(O)/(H)\quad\cos(\theta)=(A)/(H)\quad\tan(\theta)=(O)/(A)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}`

Therefore:

`\sin \theta =(3√(3))/(6√(3))=(3)/(6)=(1)/(2)`

`\cos \theta=(9)/(6√(3))=(9)/(6√(3))\cdot (√(3))/(√(3))=(9√(3))/(18)=(√(3))/(2)`

`\tan \theta=(3√(3))/(9)=(√(3))/(3)`

Answer 2

Sine θ =
`(1)/(2)`

Cosine θ=
`(√(3))/(2)`

Tangent θ =
`(√(3))/(3)`

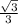
Explanation:

The formulas for sine, cosine, and tangent of an angle θ in a right triangle:

`\boxed{Sine = (Opposite )/(Hypotenuse)}`

`\boxed{Cosine =( Adjacent )/( Hypotenuse)}`

`\boxed{Tangent =( Opposite )/(Adjacent)}`

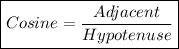
Opposite is the side of the triangle that is opposite the angle θ.

Adjacent is the side of the triangle that is adjacent to the angle θ.

Hypotenuse is the longest side of the triangle, opposite the right angle.

For Question:

In Triangle with respect to θ

Opposite=
`3√(3)`

Adjacent=9

Hypotenuse=
`6√(3)`

Now By using the Above Relation:

Sine θ =
`(3√(3))/(6√(3))=(1)/(2)`

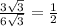
Cosine θ=
`(9)/(6√(3))=(√(3))/(2)`

Tangent θ =
`(3√(3))/(9)=(√(3))/(3)`