Question

find the equivalent resistance of the combination of resistors 1=42.0 ω, 2=75.0 ω, 3=33.0 ω, 4=61.0 ω, 5=13.5 ω, and 6=33.0 ω shown in the figure.

Answer 1

The equivalent resistance of the combination of resistors provided in the figure is 18.81Ω. ​

How to find the equivalent resistance?

To find the equivalent resistance of the given network of resistors, we need to analyze the circuit and combine resistors step by step, using the rules for combining resistances in series and parallel.

Resistors in series simply add up:

`\[ R_{\text{series}} = R_1 + R_2 + \ldots \]`

For resistors in parallel, the equivalent resistance \( R_{\text{parallel}} \) is found using:

`\[ \frac{1}{R_{\text{parallel}}} = (1)/(R_1) + (1)/(R_2) + \ldots \]`

Calculate these step by step using the given resistor values:

1. R_1 = 42.0

2. R_2 = 75.0 Ω

3. R_3 = 33.0 Ω

4. R_4 = 61.0 Ω

5. R_5 = 13.5 Ω

6. R_6 = 33.0 Ω

First, we calculate the equivalent resistance for R_1 and R_2 :

`\[ R_(12) = (1)/(\left((1)/(R_1) + (1)/(R_2)\right)) \]`

Then, add R_3 in series:

`\[ R_(123) = R_(12) + R_3 \]`

Calculate the equivalent resistance for
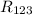`\( R_(123) \)` and R_4:

`\[ R_(1234) = (1)/(\left((1)/(R_(123)) + (1)/(R_4)\right)) \]`

Add R_5 in series:

`\[ R_(12345) = R_(1234) + R_5 \]`

Finally, calculate the equivalent resistance for
`\( R_(12345) \)` and R_6:

`\[ R_{\text{equivalent}} = (1)/(\left((1)/(R_(12345)) + (1)/(R_6)\right)) \]`

=
`\( 18.81 \Omega`