To evaluate the expression
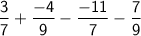 , we can follow these steps:
, we can follow these steps:
Step 1: Find a common denominator for all the fractions. In this case, the common denominator is 63, which is the least common multiple of 7 and 9.
Step 2: Convert all the fractions to have the common denominator of 63.
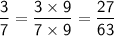
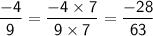
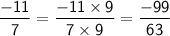
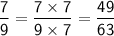
Step 3: Substitute the converted fractions back into the original expression and simplify:
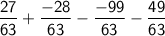
Combining the numerators over the common denominator:
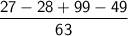
Simplifying the numerator:
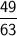
The resulting fraction is already in simplest form. Therefore, the expression
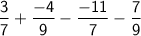 evaluates to
evaluates to
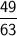 .
.