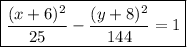Question

Determine the equation of the hyperbola with foci... 100pts

Answer 1

`((x+6)^2)/(25)-((y+8)^2)/(144)=1`

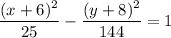
Explanation:

To write the equation of the hyperbola with foci (7, -8) and (-19, -8), and vertices (-1, -8) and (-11, -8), we first need to determine the orientation of the hyperbola.

As the y-values of the foci are the same, the foci are located horizontally from the center of the hyperbola, and therefore the hyperbola is horizontal (opening left and right).

The standard equation for a horizontal hyperbola is:

`\boxed{((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1}`

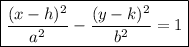
where:

• center = (h, k)
• vertices = (h±a, k)
• foci = (h±c, k) where c² = a² + b²

The center of a hyperbola is the midpoint of the vertices.

Given that the vertices are (-1, -8) and (-11, -8), we can use the midpoint formula to find the coordinates of the center:

`(h,k)=\left((x_2+x_1)/(2),(y_2+y_1)/(2)\right)`

`(h, k)=\left((-1-11)/(2),(-8-8)/(2)\right)`

`(h, k)=\left(-6,-8\right)`

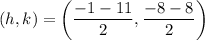
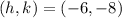
The value of "a" is the distance between the center of the hyperbola and each vertex. To find the value of a, calculate the distance between the x-coordinates:

`a=-1-(-6)=5`

`a=-6-(-11)=5`

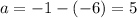
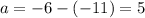
The value of "c" is the distance between the center of the hyperbola and each focus. Given that the foci are (7, -8) and (-19, -8), and the center is (-6, -8), to find the value of c, calculate the distance between the x-coordinates:

`c = 7-(-6)=13`

`c = -6-(-19)=13`

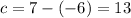
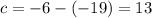
Now we have determined the values of a and c, we can use c² = a² + b² to find the value of b:

`c^2 = a^2 + b^2`

`13^2 = 5^2 + b^2`

`169 = 25 + b^2`

`b^2=144`

`b=12`

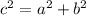
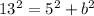
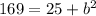
Finally, substitute the found values of a, b, h and k into the standard equation of a hyperbola:

`((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1`

`((x-(-6))^2)/(5^2)-((y-(-8))^2)/(12^2)=1`

`((x+6)^2)/(25)-((y+8)^2)/(144)=1`

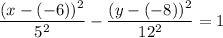
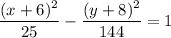
Therefore, the equation of the hyperbola with foci (7, -8) and (-19, -8), and vertices (-1, -8) and (-11, -8) is:

`\boxed{((x+6)^2)/(25)-((y+8)^2)/(144)=1}`