Answer:
Please note I have assumed the interest is compounded annually.
a) $1,262.48
b) $2,692.77
c) 7 years
d) 12 years
Explanation:
Assuming the interest is compounded annually.

Given:
Substitute the given values into the formula to create an equation for A in terms of t:
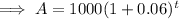
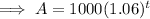
Part (a)
To calculate how much will be in the account after 4 years, substitute t = 4 into the equation:
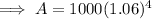
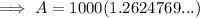
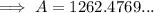
Therefore, there will be $1,262.48 in the account after 4 years.
Part (b)
To calculate how much will be in the account after 17 years, substitute t = 17 into the equation:
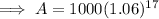

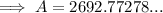
Therefore, there will be $2,692.77 in the account after 17 years.
Part (c)
To calculate how many years it will take for the account to contain $1,500, substitute A = 1500 into the equation and solve for t:

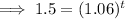
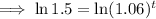
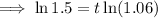
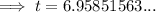
Therefore, it would take 7 years for the account to contain $1,500.
Part (d)
To calculate how many years it will take for the account to contain $2,000, substitute A = 2000 into the equation and solve for t:
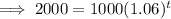
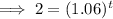
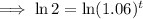
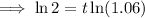

Therefore, it would take 12 years for the account to contain $2,000.