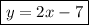Question

2x^2+3x+5/x+5

Find slant asymptote

Answer 1

To find the slant asymptote of the given function, we can perform long division of the polynomial in the numerator by the polynomial in the denominator.

2x - 7

-------------

x + 5|2x^2 + 3x + 5

2x^2 + 10x

-------------

-7x + 5

-7x - 35

--------

40

The quotient is 2x - 7 and the remainder is 40/(x+5). The slant asymptote is the quotient, which is 2x - 7.

Therefore, the slant asymptote of the function 2x^2 + 3x + 5/(x+5) is y = 2x - 7.

Hope it's understandble...

Answer 2

y = 2x + 7

Explanation:

A slant asymptote is a type of asymptote that occurs in certain rational functions when the degree of the numerator polynomial is exactly one greater than the degree of the denominator polynomial.

A slant asymptote is a straight line in the form y = mx + c, and its equation is the quotient of the division of the numerator of the function by its denominator.

Therefore, to find the equation of the slant asymptote of the given rational function, divide the numerator 2x² + 3x + 5 by the denominator (x + 5).

`\large \begin{array}{r}2x-7\phantom{))}\\x+5{\overline{\smash{\big)}\,2x^2+3x+5\phantom{))}}\\{-~\phantom{(}\underline{(2x^2+10x)\phantom{-b)}}\\-7x+5\phantom{))}\\-~\phantom{()}\underline{(-7x-35)\phantom{}}\\40\phantom{)}\\\end{array}`

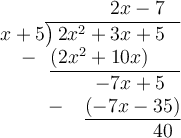
The quotient of the division is 2x - 7.

Therefore, the equation of the slant asymptote is:

`\boxed{y=2x-7}`