Question

In this problem, we explore the effect on the standard deviation of adding the same constant to each data value in a data set. Consider the following data set.

13, 9, 17, 15, 3
(a)
Use the defining formula, the computation formula, or a calculator to compute s. (Round your answer to four decimal places.)
s =
(b)
Add 3 to each data value to get the new data set 16, 12, 20, 18, 6. Compute s. (Round your answer to four decimal places.)
s =
(c)
Compare the results of parts (a) and (b). In general, how do you think the standard deviation of a data set changes if the same constant is added to each data value?
Adding the same constant c to each data value results in the standard deviation decreasing by c units.
Adding the same constant c to each data value results in the standard deviation increasing by c units.
Adding the same constant c to each data value results in the standard deviation remaining the same.
There is no distinct pattern when the same constant is added to each data value in a set.

Answer 1

(a) To compute the standard deviation (s) of the given data set {13, 9, 17, 15, 3}, we can use the formula for sample standard deviation:

`\sf s = \sqrt{\frac{\sum{(x_i - \bar{x})^2}}{n-1}}`

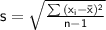
where
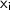`\sf x_i` are the data values,
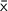`\sf \bar{x}` is the sample mean, and
`\sf n` is the number of data values.

First, let's calculate the sample mean:

`\sf \bar{x} = (13 + 9 + 17 + 15 + 3)/(5) = 11.4`

Next, calculate the sum of squared differences:

`\sf \sum{(x_i - \bar{x})^2} = (13-11.4)^2 + (9-11.4)^2 + (17-11.4)^2 + (15-11.4)^2 + (3-11.4)^2 = 80.8`

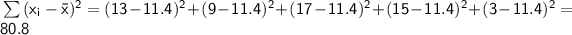
Now we can plug these values into the formula for sample standard deviation:

`\sf s = \sqrt{(80.8)/(5-1)} \approx √(20.2) \approx 4.4934`

So, the standard deviation (s) of the given data set is approximately 4.4934.

(b) For the new data set {16, 12, 20, 18, 6}, we can follow the same steps to compute the standard deviation (s):

Calculate the sample mean:

`\sf \bar{x} = (16 + 12 + 20 + 18 + 6)/(5) = 14.4`

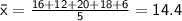
Calculate the sum of squared differences:

`\sf \sum{(x_i - \bar{x})^2} = (16-14.4)^2 + (12-14.4)^2 + (20-14.4)^2 + (18-14.4)^2 + (6-14.4)^2 = 72.8`

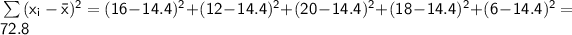
Plug these values into the formula for sample standard deviation:

`\sf s = \sqrt{(72.8)/(5-1)} \approx √(18.2) \approx 4.2691`

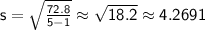
So, the standard deviation (s) of the new data set is approximately 4.2691.

(c) Comparing the results of parts (a) and (b), we can observe that adding the same constant (in this case, 3) to each data value does not change the standard deviation. The standard deviation remains the same. This is a general property of adding a constant to each data value in a data set.