Question

The area of a rectangle is 3x2 - 12x square yards. If the width is 3x yards, what is the length of the rectangle?

Answer 1

Answer: The length of the rectangle is x - 4 yards.

Explanation:

We can create an equation to solve this word problem, where the variable L = length.

3x × L =
`3x^2 - 12x`

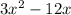
We need to solve for the variable L, to find the length of the rectangle.

First lets factor the right side of the equation to make it easier to divide with.

3x × L =
`3x^2 - 12x`

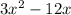
We can factor out 3x from the right side of the equation.

3x × L = 3x(x - 4)

Now we need to get the variable L by itself (isolating the variable). In order to do that, we can divide both sides by 3x.

3x × L = 3x(x - 4)

/3x /3x

L = x - 4

The length of the rectangle is x - 4 yards.

Answer 2

x - 4 yards.

Explanation:

Given:

Area of rectangle = 3x^2 - 12x square yards

Width = 3x yards

To find:

Length of rectangle

Solution:

The area of a rectangle is equal to the product of its length and width.

Area of rectangle = Length * Width

Substituting the given values, we get:

3x^2 - 12x = Length * 3x

Length =( 3x^2 - 12x )3x

Length = x-4

Therefore, the length of the rectangle is x - 4 yards.