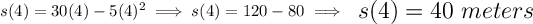Question

The location x of a car in meters is given by the function

x=30t−5t^2, where t is in seconds. At the time when the car is moving at 10 m/s in the direction opposite to its initial motion, how far is the car from where it was at t = 0? Show all your work.

Answer 1

well, we can look at it this way

the car has an equation, a positional equation, and since it's in "t" terms we can just call it s(t), and we know that s(t) = 30t - 5t², now let's recall that the derivative of the positional equation simply gives us the velocity equation, hmmm the derivative of that is simple enough is just 30 - 10t pretty much using the power rule, no fuss there.

now, let's look at all that jumbled wording, "At the time when the car is moving at 10 m/s in the direction opposite to its initial motion", the hell is that?

well, is another way to say, hmmmm if the car goes in an opposite direction to initial, that gives us a negative rate, this rate is 10 m/s, which oddly enough is velocity, and is negative, so is really -10 m/s, so we can just reword that as "when the velocity of this car is negative 10", let's put all that in differentiation terms

`s(t)=30t-5t^2\implies \stackrel{velocity}{\cfrac{ds}{dt}=30-10t}\implies \stackrel{\textit{velocity is -10}}{-10=30-10t}\implies 4=t`

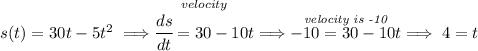
now the car at t=0 is just s(0) = 0, so how far is the car at t = 4?

`s(4)=30(4)-5(4)^2\implies s(4)=120-80\implies {\Large \begin{array}{llll} s(4)=40~meters \end{array}}`