Question

To practice Problem-Solving Strategy 27. 2 Motion in Magnetic Fields. An electron inside of a television tube moves with a speed of 2. 74×107 m/s. It encounters a region with a uniform magnetic field oriented perpendicular to its trajectory. The electron begins to move along a circular arc of radius 0. 190 m. What is the magnitude of the magnetic field?Part CCalculate the magnitude F of the force exerted on the electron by a magnetic field of magnitude 8. 21×10−4 T oriented as described in the problem introduction. Express your answer in newtons

Answer 1

Magnetic field strength: approximately
`8.20 * 10^(-4)\; {\rm T}`.

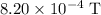Force on the electron: approximately
`3.60 * 10^(-15)\; {\rm N}`.

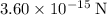Step-by-step explanation:

Look up the charge and mass of an electron:

• The magnitude of charge on an electron is the same as the elementary charge:
  `q_(e) \approx 1.602 * 10^(-19)\; {\rm C}`.
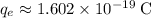• Electron rest mass:
  `m_(e) \approx 9.109 * 10^(-31)\; {\rm kg}`.

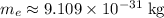Since the electron is moving perpendicularly across a magnetic field, magnitude of the magnetic force on this electron would be:

`F = q\, v\, B`,

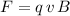Where:

• 
  `q` is the magnitude of the electric charge on this electron,
• 
  `v` is the speed of the electron, and
• 
  `B` is the magnitude of the magnetic field.

At the same time, because the electron is in a centripetal motion, magnitude of the net force on the electron should satisfy:

`\displaystyle F_{\text{net}} = (m\, v^(2))/(r)`,

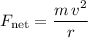Where:

• 
  `m` is the mass of the electron,
• 
  `v` is the speed of the electron, and
• 
  `r` is the radius of the circular orbit.

Assuming that magnetic force from the field is the only force on this point charge. Net force on the charge would be equal to the magnetic force. In other words:

`\displaystyle (m\, v^(2))/(r) = q\, v\, B`.

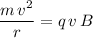Rearrange this equation and solve for the magnetic field strength:

`\begin{aligned}B &= (m\, v)/(q\, r) \\ &\approx ((9.109 * 10^(-31))\, (2.74 * 10^(7)))/((1.602 * 10^(-19))\, (0.190))\; {\rm T} \\ &\approx 8.20 * 10^(-4)\; {\rm T}\end{aligned}`.

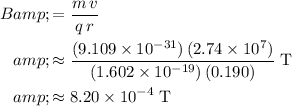Substitute
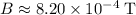`B \approx 8.20 * 10^(-4)\; {\rm T}` back into the equation
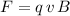`F = q\, v\, B` to find the magnetic force on this electron:

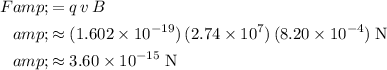`\begin{aligned}F &= q\, v\, B \\ &\approx (1.602 * 10^(-19))\, (2.74 * 10^(7))\, (8.20 * 10^(-4))\; {\rm N}\\ &\approx 3.60 * 10^(-15)\; {\rm N}\end{aligned}`.