Question

You have two unknown integers. Double the larger integer increased by triple the smaller integer is 46. Squaring the larger number and increasing it by four times itself gives the same result as multiplying the smaller number by 20 and adding 5. Use a system to solve for the integers by graphing

Answer 1

To solve the system of equations for the unknown integers, set up the equations based on the given information and solve the system graphically by finding the intersection point on a graph.

Step-by-step explanation:

To solve for the unknown integers, we can set up a system of equations based on the given information.

Let's assume the larger integer is x and the smaller integer is y.

From the first statement, we have the equation: 2x + 3y = 46.

From the second statement, we have the equation: x^2 + 4x = 20y + 5.

To solve this system of equations graphically, we can plot the two equations on a graph and find the intersection point, which represents the solution.

By finding the coordinates of the intersection point, we can determine the values of x and y.

Answer 2

The solutions for x and y as ordered pairs are (19, 4) and (7, 9).

Let's denote the larger integer as x and the smaller integer as y. Write down the two equations based on the problem.

The two equations are: 2x + 3y = 46 and x² + 4x = 20y + 5.

Rearrange the first equation to solve for x.

The rearranged first equation is
`x = ((46 - 3y))/(2)`.

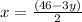Substitute x from the rearranged first equation into the second equation.

The substituted second equation is
`(((46 - 3y))/(2) )^2 + 4(((46 - 3y))/(2) ) = 20y + 5`.

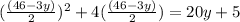Simplify the substituted second equation.

The simplified equation is y² - 23y + 36 = 0.

Solve the quadratic equation y² - 23y + 36 = 0 for y.

The solutions for y are y = 4 and y = 9.

Substitute each solution for y back into the rearranged first equation to solve for x.

The solutions for x are x = 19 when y = 4 and x = 7 when y = 9.