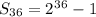Question

write an expression that gives the requested sum. the sum of the first 36 terms of the geometric sequence 1, 2, 4,

Answer 1

`S_(36)=2^3^6-1`

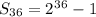
Explanation:

The formula for sum of a finite geometric series (aka a geometric series that has a finite number of terms, including a first and last term) is given by:

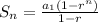`S_(n) =(a_(1)(1-r^n) )/(1-r)`, where

• Sn is the sum of n number of terms (e.g. 36 terms),
• a1 is the first term,
• r is the common ratio,
• and n is the number of terms in the series.

Step 1: Find the common ratio:

In order to find the common ratio, we divide two consecutive terms in the series, with a succeeding term being divide by a preceding term. Thus, we can divide 2 by 1: 2 / 1 = 2.

Thus, the common ratio is 2.

Step 2: Plug in values.

Our first term is 36, the common ratio is 2, and there are 36 terms in the series. Now we can plug these values into the formula and simplify:

`S_(36) =(1(1-2^3^6) )/(1-2)\\S_(36) =(1-2^3^6)/(-1)\\ S_(36)=2^3^6-1`

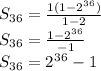
Thus, the expression that gives the requested sum is

`S_(36)=2^3^6-1`