Question

NO LINKS!!

The populations P (in thousands) of a city from 2000 through 2020 can be modeled by

P = 2687/(1 + 0.089e^0.050t) where t represents the year, with t = 0 corresponding to 2000.

a. Use the model to find the population of the city (in thousands) in the years 2001, 2006, 2011, 2015, and 2020. (Round your answers to 3 decimal places.)

2001 P = ______________ thousand people
2006 P= ______________ thousand people
2011 P = ______________ thousand people
2015 P= ______________ thousand people
2020 P= _____________ thousand people

b. Use a graphing utility to graph the function to determine the year in which the population reached 2.2 million
The population will reach 2.2 million in __________.

c. Confirm your answer to part (b) algebraically.
The population will reach 2.2 million in __________.

Answer 1

a) 2001: P = 2457.106 thousand people

2006: P = 2398.813 thousand people

2011: P = 2327.899 thousand people

2015: P = 2260.998 thousand people

2020: P = 2163.573 thousand people

b) 2018

c) 2018

Explanation:

Given function:

`P = (2687)/(1 + 0.089e^(0.050t))`

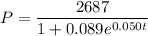
where:

• P = population (in thousands)
• t = number of years after the year 2000

Part (a)

In 2001, t = 1:

`\begin{aligned}t = 1 \implies P &= (2687)/(1 + 0.089e^(0.050(1)))\\\\&= (2687)/(1 + 0.089e^(0.050))\\\\&=2457.106 \; \sf (3 \; d.p.)\end{aligned}`

In 2006, t = 6:

`\begin{aligned}t = 6 \implies P &= (2687)/(1 + 0.089e^(0.050(6)))\\\\&= (2687)/(1 + 0.089e^(0.3))\\\\&=2398.813 \; \sf (3 \; d.p.)\end{aligned}`

In 2011, t = 11:

`\begin{aligned}t = 11 \implies P &= (2687)/(1 + 0.089e^(0.050(11)))\\\\&= (2687)/(1 + 0.089e^(0.55))\\\\&=2327.899 \; \sf (3 \; d.p.)\end{aligned}`

In 2015, t = 15:

`\begin{aligned}t = 15 \implies P &= (2687)/(1 + 0.089e^(0.050(15)))\\\\&= (2687)/(1 + 0.089e^(0.75))\\\\&= 2260.998\; \sf (3 \; d.p.)\end{aligned}`

In 2020, t = 20:

`\begin{aligned}t = 20 \implies P &= (2687)/(1 + 0.089e^(0.050(20)))\\\\&= (2687)/(1 + 0.089e^(1))\\\\&=2163.573 \; \sf (3 \; d.p.)\end{aligned}`

Part (b)

See attached for the graph of the function.

2.2 million = 2,200,000 = 2200 thousand

Therefore, draw a line at y = 2200.

The point of intersection between P(t) and y = 2200 is (18.223, 2200).

Therefore, the population will reach 2.2 million during 2018.

`\implies (2687)/(1 + 0.089e^(0.050t))=2200`

`\implies 2687=2200(1 + 0.089e^(0.050t))`

`\implies (2687)/(2200)=1 + 0.089e^(0.050t)`

`\implies (2687)/(2200)-1=0.089e^(0.050t)`

`\implies (487)/(2200)=0.089e^(0.050t)`

`\implies \ln \left((487)/(2200)\right)=\ln \left(0.089e^(0.050t)\right)`

`\implies \ln \left((487)/(2200)\right)=\ln \left(0.089 \right)+\ln \left(e^(0.050t)\right)`

`\implies \ln \left((487)/(2200)\right)=\ln \left(0.089 \right)+0.050t`

`\implies \ln \left((487)/(2200)\right)-\ln \left(0.089 \right)=0.050t`

`\implies \ln \left((2435)/(979)\right)=0.050t`

`\implies t=20\ln \left((2435)/(979)\right)`

`\implies t=18.223\; \sf (3 \; d.p.)`

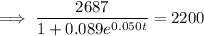
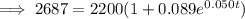
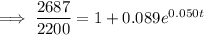
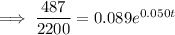
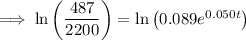
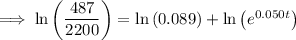
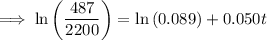
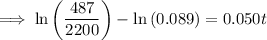
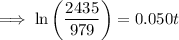
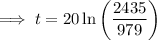
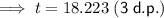
The population will reach 2.2 million in 2018.