Question

Solve this question
i need it

Answer 1

To find the limit of a convergent sequence, we can simply take the limit as n approaches infinity. Let's calculate the limits for each of the given sequences:

A.
`\sf\:\lim_(n \to \infty) (5n)/(n+7) \\`

To find the limit, we divide the leading terms by n:

`\sf\:\lim_(n \to \infty) (5n/n)/((n+7)/n) = (5)/(1) = 5 \\`

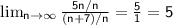
Therefore, the limit of the sequence A is 5.

B.
`\sf\:\lim_(n \to \infty) (4-7n)/(8+n) \\`

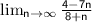
Again, divide the leading terms by n:

`\sf\:\lim_(n \to \infty) (4/n - 7)/(8/n + 1) = (0 - 7)/(0 + 1) = -7 \\`

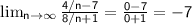
So, the limit of sequence B is -7.

C.
`\sf:\lim_(n \to \infty) (8n - 500√(n))/(2n + 800√(n)) \\`

Divide the leading terms by n:

`\sf\:\lim_(n \to \infty) (8 - 500√(n)/n)/(2 + 800√(n)/n) \\`

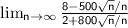
As n approaches infinity, the terms involving
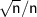`\sf\:√(n)/n \\` tend to 0:

`\sf\:\lim_(n \to \infty) (8 - 500(0))/(2 + 800(0)) = (8)/(2) = 4 \\`

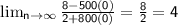
Therefore, the limit of sequence C is 4.

To summarize:

A. The limit of sequence A is 5.

B. The limit of sequence B is -7.

C. The limit of sequence C is 4.