Question

NO LINKS!! (NOT MULTIPLE CHOICE)

Use the formula A = P( 1 + r/n)^(nt) to calculate the balance A of an investment (in dollars) when P = $4000, r = 4%, and t= 10years, and compunding is done by the day, by the hour, by the minute, and by the second. (Round your answers to the nearest cent).

a. compounding by the day: A= $

b. compounding by the hour: A= $

c. compounding by the minute: A= $

d. compounding by the second: A= $


Does increasing the number of compoundings per year result in unlimited growth of the balance? yes or no (choose one)

Answer 1

a. compounding by the day: A = $5967.17

b. compounding by the hour: A = $5967.29

c. compounding by the minute: A = $5967.30

d. compounding by the second: A = $5967.30

Explanation:

`\boxed{\begin{minipage}{8.5 cm}\underline{Compound Interest Formula}\\\\$ A=P\left(1+(r)/(n)\right)^(nt)$\\\\where:\\\\ \phantom{ww}$\bullet$ $A =$ final amount \\ \phantom{ww}$\bullet$ $P =$ principal amount \\ \phantom{ww}$\bullet$ $r =$ interest rate (in decimal form) \\ \phantom{ww}$\bullet$ $n =$ number of times interest is applied per year \\ \phantom{ww}$\bullet$ $t =$ time (in years) \\ \end{minipage}}`

Part (a)

If the interest is compounding by the day then n = 365.

Given:

• P = $4000
• r = 4% = 0.04
• n = 365
• t = 10 years

Substitute the values into the compound interest formula and solve for A:

`\implies A=4000\left(1+(0.04)/(365)\right)^(365 * 10)`

`\implies A=4000\left(1.00010958...\right)^(3650)`

`\implies A=4000(1.49179200...)`

`\implies A=5967.16801...`

`\implies A=\$5967.17`

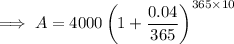
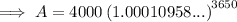
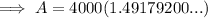
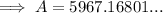
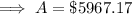
Part (b)

If the interest is compounding by the hour then:

• n = 365 × 24 = 8760

Given:

• P = $4000
• r = 4% = 0.04
• n = 8760
• t = 10 years

Substitute the values into the compound interest formula and solve for A:

`\implies A=4000\left(1+(0.04)/(8760)\right)^(8760 * 10)`

`\implies A=4000\left(1.00000456...\right)^(87600)`

`\implies A=4000\left(1.49182333...\right)`

`\implies A=5967.29333...`

`\implies A=\$5967.29`

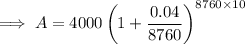
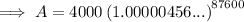
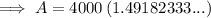
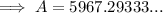
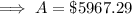
Part (c)

If the interest is compounding by the minute then:

• n = 365 × 24 × 60 = 525600

Given:

• P = $4000
• r = 4% = 0.04
• n = 525600
• t = 10 years

Substitute the values into the compound interest formula and solve for A:

`\implies A=4000\left(1+(0.04)/(525600)\right)^(525600 * 10)`

`\implies A=4000\left(1.00000007...\right)^(5256000)`

`\implies A=4000(1.49182466...)`

`\implies A=5967.29867...`

`\implies A=\$5967.30`

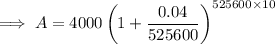
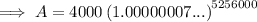
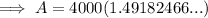
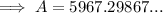
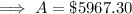
Part (d)

If the interest is compounding by the second then:

• n = 365 × 24 × 60 × 60 = 31536000

Given:

• P = $4000
• r = 4% = 0.04
• n = 31536000
• t = 10 years

Substitute the values into the compound interest formula and solve for A:

`\implies A=4000\left(1+(0.04)/(31536000)\right)^(31536000 * 10)`

`\implies A=4000\left(1.00000000...\right)^(315360000)`

`\implies A=4000\left(1.49182390...\right)`

`\implies A=5967.29562...`

`\implies A=\$5967.30`

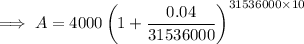
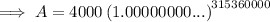
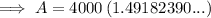
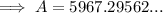
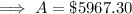
The more compounding periods throughout the year, the higher the future value of the investment. However, the difference between compounding by the day and compounding by the second results in a difference of 13 cents over the year, which is negligible comparatively.