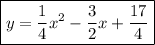Question

Write the equation of a quadratic with a vertex at (3,2) and directrix of y=1

Answer 1

`\textsf{Standard form (quadratic):} \quad y=(1)/(4)x^2-(3)/(2)x+(17)/(4)`

`\textsf{Standard form (parabola):} \quad (x-3)^2=4(y-2)`

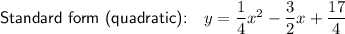
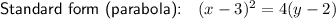
Explanation:

A quadratic function is a parabola with a vertical axis of symmetry.

The standard formula of a parabola with a vertical axis of symmetry is:

`\large{\boxed{(x-h)^2=4p(y-k)}`

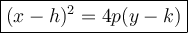
where:

• p ≠ 0
• Vertex = (h, k)
• Focus = (h, k+p)
• Directrix: y = (k - p)
• Axis of symmetry: x = h

If the parabola opens upwards then p > 0, and if the parabola opens downwards then p < 0.

Given the vertex is at (3, 2):

• h = 3
• k = 2

Given the directrix is y = 1 and k = 2, we can use the formula for the directrix to calculate the value of p:

`\begin{aligned}y&=k-p\\\implies 1&=2-p\\p&=2-1\\p&=1\end{aligned}`

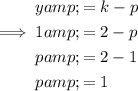
Therefore, the value of p is 1 (and the parabola opens upwards).

Substitute the values of h, k and p into the standard formula:

`(x-3)^2=4(1)(y-2)`

`(x-3)^2=4(y-2)`

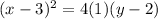
Expand and rearrange the equation into the standard form of a quadratic equation, y = ax² + bx + c:

`\begin{aligned}(x-3)^2&=4(y-2)\\x^2-6x+9&=4y-8\\x^2-6x+9+8&=4y-8+8\\x^2-6x+17&=4y\\y&=(1)/(4)x^2-(3)/(2)x+(17)/(4)\end{aligned}`

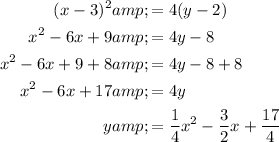
Therefore, the equation of a quadratic in standard form with a vertex at (3, 2) and directrix of y = 1 is:

`\boxed{y=(1)/(4)x^2-(3)/(2)x+(17)/(4)}`

Answer 2

`y = ((x-3)^2)/(4) + 2`

Explanation:

We are given that the directrix of the quadratic function (parabola) is the horizontal line
`y=1`.

And, because the vertex is above the directrix (its y-coordinate is
`> 1`), we know that the parabola opens upwards.

In the standard form equation for a quadratic (centered at the origin):

`x^2 = 4py`,

`p` is the shortest distance from the vertex to the directrix. This distance is the same as from the vertex to the focus.

We can solve for
`p` for this quadratic by subtracting the y-value of the directrix from the y-coordinate of the vertex:

`p=2-1`

`p=1`

Finally, we can construct the equation of the quadratic using that
`p`-value:

`(x-3)^2 = 4(1)(y-2)`

`(x-3)^2 = 4(y-2)`

We can also simplify by solving for y:

`(x-3)^2 = 4y-8`

`(x-3)^2 + 8 = 4y`

`\boxed{y = ((x-3)^2)/(4) + 2}`