Question

Suppose P(t)represents the population of a certain mosquito colony, where. t is measured in days. The current population of the colony is known to be 574 mosquitos; that is, P(0)=574. If P'(0)=50 mosquitos per day, estimate the size of the population in 10 days.

Answer 1

The estimated size of the population in 10 days is of 1372 mosquitos.

Explanation:

Population after t days:

The population after t days is given by:

`P(t) = P(0)e^(rt)`

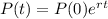
In which P(0) is the initial population and r is the growth rate, as a decimal.

P(0)=574.

So

`P(t) = 574e^(rt)`

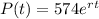
P'(0)=50

`P^(\prime)(t) = 574re^(rt)`

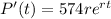
Since P'(0)=50

`574r = 50`

`r = (50)/(574)`

`r = 0.0871`

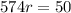
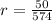
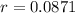
So

`P(t) = 574e^(0.0871t)`

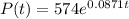
Estimate the size of the population in 10 days

This is P(10).

`P(10) = 574e^(0.0871*10) = 1372`

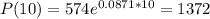
The estimated size of the population in 10 days is of 1372 mosquitos.