Question

Rahul is deciding between two parking garages. Garage A charges an initial fee of $12 to park plus $4 per hour. Garage B charges an initial fee of $6 to park plus $5 per hour. Let AA represent the amount Garage A would charge if Rahul parks for tt hours, and let BB represent the amount Garage B would charge if Rahul parks for tt hours. Write an equation for each situation, in terms of t,t, and determine which garage would be cheaper if Rahul needs to park for 10 hours.

Answer 1

1. AA = 4t + 12

2. BB = 5t + 6

3. Garage A would be cheaper to park for 10 hours.

Explanation:

1. Garage A's situation is linear, meaning that there is a constant rate of change, or slope.

A linear function in slope-intercept form is:
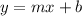`y = mx + b`, where m is the rate of change, and b is the y-intercept, or the initial value.

1. Find m and b:
2. m = 4 because that is the cost per hour, which is additive and constant
3. b = 12 because it is the initial cost Rahul has to pay
4. ∴ AA = 4x + 12

2. Garage B's situation is linear, meaning that there is a constant rate of change, or slope.

A linear function in slope-intercept form is:
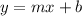`y = mx + b`, where m is the rate of change, and b is the y-intercept, or the initial value.

1. Find m and b:
2. m = 5 because that is the cost per hour, which is additive and constant
3. b = 6 because it is the initial cost Rahul has to pay
4. ∴ AA = 5x + 6

3. To find how much it will cost Rahul to park in Garages A and B for 10 hours, substitute 10 into t, which is the number of hours. Then, determine which cost is lower.

1. Garage A for 10 hours:
2. AA = 4t + 12
3. AA = 4(10) + 12
4. AA = 40 + 12
5. ∴ AA = $52
6. Garage B for 10 hours:
7. BB = 5t + 6
8. BB = 5(10) + 6
9. BB = 50 + 6
10. ∴ BB = $56
11. $52 < $56, so Garage A is cheaper for 10 hours.