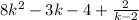Answer:
Explanation:
⭐ See the image I attached to my answer to see the working.
⭐ I recommend you look at the image while following along with the steps to understand the steps.
1. See what multiplies with the first term in the divisor to get the first term in the dividend. Then, put that answer in the quotient space.
2. Under the first term in the dividend, write a - sign and open parentheses. Put the first term inside the parentheses.
3. Multiply what you put in the quotient space from step #1 with the second term in the divisor.
4. Put the product from step #3 inside of the parentheses.
5. Subtract the first two terms in the parentheses from the first two terms in the dividend.
. . . . . . . . . . . . . note: in polynomial division, you will not always subtract two terms. we are subtracting two terms here because there are two terms in the divisor.
6. Write the answer from #5 under the parentheses, and bring down another term from the dividend.
7. See what multiplies with the first term in the dividend to get the answer from #5. Then, put that answer in the quotient space.
8. Under step #6, write a - sign and open parentheses. Put the answer from #5 inside the parentheses.
9. Multiply the answer from #7 with the second term in the divisor.
10. Next to the answer from step #8, write the product of step #9.
11. Subtract the terms from step #10 from step #6.
12. Repeat until you have "brought down" all of the terms from the dividend.
After you are done, your remainder will not be 0. Instead, it will be +2. When you have a remainder that isn't 0, you cannot use the quotient as your answer. Instead, you have to write your answer in this format:
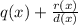, where q(x) is the quotient, r(x) is the remainder, and d(x) is the divisor.
⇒ q(x) =
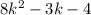
⇒ r(x) = +2
⇒ d(x) = k -2
⇒