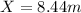Question

Suppose that the separation between two speakers A and B is 4.80 m and the speakers are vibrating in-phase. They are playing identical 134-Hz tones and the speed of sound is 343 m/s. An observer is seated at a position directly facing speaker B in such a way that his line of sight extending to B is perpendicular to the imaginary line between A and B. What is the largest possible distance between speaker B and the observer, such that he observes destructive interference

Answer 1

`X=8.44m`

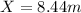
Step-by-step explanation:

From the question we are told that

Distance b/w A&B
`x=4.80m`

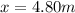
Frequency
`f=134Hz`

Sound speed
`v=343m/s`

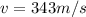
Generally the equation for wavelength is mathematically given as

`\lambda=v/f`

`\lambda/2=1/2*v/f`

`\lambda/2=1/2*(343)/(135)`

`\lambda/2=1.27037037`

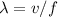
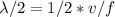
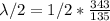
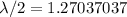
Generally the destructive interference X is mathematically given by

`√(4.8^2 +X^2) -X=1.27037037\\`

`23.04+BC^2=X^2+1.613+2.54*X`

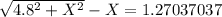
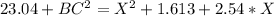
Therefore the destructive interference is

`X=8.44m`