Question

A savings account earns interest by being compounded continuously. The account initially had $1,500 deposited in it. The worth of the account after t-years can be calculated using the formula: A(t)=1500e.03t

(Part A)By what percent will the worth of the account increase per year? Round to the nearest hundredth of a percent (Part B) To the nearest tenth of a year, how many years will it take for the worth of the account to double?
(Part C) If another investment began with a principal of $1,200 and earned interest of 4.5% applied once per year, which investment would be worth more after 10 years?

Answer 1

The worth of the account will increase by 3% per year. It will take approximately 23.1 years for the worth of the account to double. The first investment would be worth more after 10 years.

Step-by-step explanation:

(Part A) To find the percentage increase per year, we need to determine the annual growth rate. In this case, the growth rate is given by the exponent in the formula, which is 0.03. To convert this to a percentage, we multiply by 100: 0.03 * 100 = 3%. Therefore, the worth of the account will increase by 3% per year.

(Part B) To find how many years it will take for the worth of the account to double, we need to set up an equation. We can use the formula for compound interest to solve for t:

2 * 1500 = 1500 *
`e^((0.03t))`

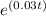
Dividing both sides by 1500, we get:

2 =
`e^{(0.03t)`

Using logarithms, we can solve for t:

ln(2) = 0.03t * ln(e).

ln(2) = 0.03t.

Dividing both sides by 0.03, we get:

t = ln(2) / 0.03 ≈ 23.1 years.

(Part C) To compare the two investments, we can use the formulas for continuous compounding and simple interest. For the first investment, the worth after 10 years is:

A(t) = 1500 *
`e^{(0.03 * 10)`

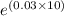
A(t) ≈ 1500 *
`2.71828^{(0.30)`99 ≈ $2,024.85.

For the second investment, the worth after 10 years is:

A(t) = 1200 * (1 + 0.045 * 10) = 1200 * (1 + 0.45) = $1,740.

Therefore, the first investment would be worth more after 10 years.

Answer 2

The worth of the account will increase by 3% per year. It will take approximately 23.1 years for the worth of the account to double. The continuously compounded interest account will have a higher value after 10 years.

Step-by-step explanation:

(Part A) To calculate the percent by which the worth of the account will increase per year, we need to find the rate of change of the function A(t). The rate of change of a continuously compounded interest rate is given by the coefficient of t, in this case, 0.03. To convert this to a percentage, we multiply by 100. So, the worth of the account will increase by 3% per year.

(Part B) To find how many years it will take for the worth of the account to double, we need to solve the equation A(t) = 2 * A(0), where A(0) is the initial worth of the account. In this case, A(0) = $1500. So, we set 1500e^(0.03t) = 2 * 1500 and solve for t. Taking the natural logarithm of both sides, we get ln(2) = 0.03t, and solving for t, we get t ≈ 23.1 years.

(Part C) To compare the two investments, we can calculate the worth of the second one after 10 years. The formula for compound interest applied once per year is A = P(1 + r/n)^(nt), where P is the principal, r is the annual interest rate in decimal form, n is the number of times interest is compounded per year, and t is the number of years. Plugging in the values P = $1200, r = 0.045, n = 1, and t = 10, we get A = 1200(1+0.045)^10 ≈ $1963.40. Comparing this to the worth of the continuously compounded interest account after 10 years, we can see that the continuously compounded interest account would have a higher value.