Question

Ridgid motions to prove

Answer 1

Sequence:

1.
`T__( < 0,-5 > ) (ABCDE) = (A'B'C'D'E)`

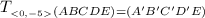
. . . . . . . . . . ⭐ please take a ruler and measure the distance from AA', . . . . . . . . BB', CC', DD', and EE', and then write that distance (it should . . . . . . . . be the same for each measurement) in place of 5 in -5. I just . . . . . . . . wrote -5 because it was my best approximation for looking at . . . . . . . . a laptop screen. ⭐

2.
`R__((180,B')) (A'B'C'D'E) = (A''B''C''D''E'')`

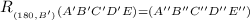
3.
`r__(D''E'') (A''B''C''D''E'') = (A'''B'''C'''D'''E''')`

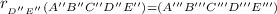
Explanation:

1.
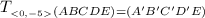`T__( < 0,-5 > ) (ABCDE) = (A'B'C'D'E)` means that when you move figure ABCDE down by 5 units, it will map onto the image of A'B'C'D'E.

2.
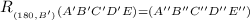`R__((180,B')) (A'B'C'D'E) = (A''B''C''D''E'')` means that when you rotate figure A'B'C'D'E' 180 degrees counterclockwise about point B', said figure will map onto the image of A''B''C''D''E''.

3.
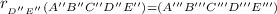`r__(D''E'') (A''B''C''D''E'') = (A'''B'''C'''D'''E''')` means that when you reflect figure A''B''C''D''E'' across segment D''E'', said figure will map onto the image A'''B'''C'''D'''E'''.