Question

catherine rolls a standard $6$-sided die five times, and the product of her rolls is $300.$ how many different sequences of rolls could there have been? (the order of the rolls matters.)

Answer 1

150 sequences

Explanation:

Let's find the sets of 5 integers less than or equal to 6 that could multiply to 300 (where order doesn't matter for right now):

1, 2, 5, 5, 6

1, 3, 4, 5, 5

2, 2, 3, 5, 5

Now let's find the number of unique ways we could reorder these sets

There are
`(5!)/(2!) = 60` ways to order {1, 2, 5, 5, 6}

There are
`(5!)/(2!) = 60` ways to order {1, 3, 4, 5, 5}

There are
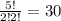`(5!)/(2!2!) = 30` ways to order {2, 2, 3, 5, 5}

There could have, therefore, been 60 + 60 + 30 = 150 different sequences of rolls