Answer:
The factored form of the polynomial is
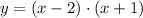 .
.
Explanation:
According to the graph, we have a second order polynomial with a vertical axis of symmetry. The standard form of the polynomial is:
 (1)
(1)
Where:
 - Independent variable.
- Independent variable.
 - Dependent variable.
- Dependent variable.
 ,
,
 ,
,
 - Coefficients.
- Coefficients.
We can obtain the solution of the polynomial by knowing three distinct points. From graph we know that the curve pass through the following three points:
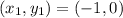 ,
,
 ,
,
 . Three linear equations are constructed:
. Three linear equations are constructed:
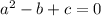 (2)
(2)
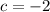 (3)
(3)
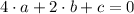 (4)
(4)
The solution of this system is
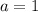 ,
,
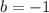 and
and
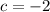 . Then, the polynomial in standard form is
. Then, the polynomial in standard form is
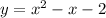 . By factorization, we find that factored form is:
. By factorization, we find that factored form is:
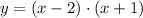 (5)
(5)