Question

Find the derivative: y={ (3x+1)cos(2x) } / e^2x​

Answer 1

`\displaystyle y' = (3cos(2x) -2(3x + 1)[sin(2x) + cos(2x)])/(e^(2x))`

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Algebra I

• Factoring
• Exponential Rule [Dividing]:
  `\displaystyle (b^m)/(b^n) = b^(m - n)`
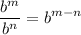
• Exponential Rule [Powering]:
  `\displaystyle (b^m)^n = b^(m \cdot n)`

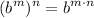
Calculus

Derivatives

Derivative Notation

Derivative of a constant is 0

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Product Rule:
`\displaystyle (d)/(dx) [f(x)g(x)]=f'(x)g(x) + g'(x)f(x)`

Quotient Rule:
`\displaystyle (d)/(dx) [(f(x))/(g(x)) ]=(g(x)f'(x)-g'(x)f(x))/(g^2(x))`

Trig Derivative:
`\displaystyle (d)/(dx)[cos(u)] = -u'sin(u)`

eˣ Derivative:
`\displaystyle (d)/(dx)[e^u] = u'e^u`

Explanation:

Step 1: Define

`\displaystyle y = ((3x + 1)cos(2x))/(e^(2x))`

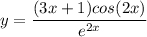
Step 2: Differentiate

1. [Derivative] Quotient Rule:
   `\displaystyle y' = ((d)/(dx)[(3x + 1)cos(2x)]e^(2x) - (d)/(dx)[e^(2x)](3x + 1)cos(2x))/((e^(2x))^2)`
2. [Derivative] [Fraction - Numerator] eˣ derivative:
   `\displaystyle y' = ((d)/(dx)[(3x + 1)cos(2x)]e^(2x) - 2e^(2x)(3x + 1)cos(2x))/((e^(2x))^2)`
3. [Derivative] [Fraction - Denominator] Exponential Rule - Powering:
   `\displaystyle y' = ((d)/(dx)[(3x + 1)cos(2x)]e^(2x) - 2e^(2x)(3x + 1)cos(2x))/(e^(4x))`
4. [Derivative] [Fraction - Numerator] Product Rule:
   `\displaystyle y' = ([(d)/(dx)[3x + 1]cos(2x) + (d)/(dx)[cos(2x)](3x + 1)]e^(2x) - 2e^(2x)(3x + 1)cos(2x))/(e^(4x))`
5. [Derivative] [Fraction - Numerator] [Brackets] Basic Power Rule:
   `\displaystyle y' = ([(1 \cdot 3x^(1 - 1))cos(2x) + (d)/(dx)[cos(2x)](3x + 1)]e^(2x) - 2e^(2x)(3x + 1)cos(2x))/(e^(4x))`
6. [Derivative] [Fraction - Numerator] [Brackets] (Parenthesis) Simplify:
   `\displaystyle y' = ([3cos(2x) + (d)/(dx)[cos(2x)](3x + 1)]e^(2x) - 2e^(2x)(3x + 1)cos(2x))/(e^(4x))`
7. [Derivative] [Fraction - Numerator] [Brackets] Trig derivative:
   `\displaystyle y' = ([3cos(2x) -2sin(2x)(3x + 1)]e^(2x) - 2e^(2x)(3x + 1)cos(2x))/(e^(4x))`
8. [Derivative] [Fraction - Numerator] Factor:
   `\displaystyle y' = (e^(2x)[(3cos(2x) -2sin(2x)(3x + 1)) - 2(3x + 1)cos(2x)])/(e^(4x))`
9. [Derivative] [Fraction] Simplify [Exponential Rule - Dividing]:
   `\displaystyle y' = (3cos(2x) -2sin(2x)(3x + 1) - 2(3x + 1)cos(2x))/(e^(2x))`
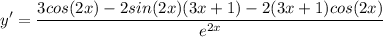
10. [Derivative] [Fraction - Numerator] Factor:
    `\displaystyle y' = (3cos(2x) -2(3x + 1)[sin(2x) + cos(2x)])/(e^(2x))`

Topic: AP Calculus AB/BC

Unit: Derivatives

Book: College Calculus 10e