Question

Consider a circle whose equation is x2 + y2 – 2x – 8 = 0. Which statements are true? Select three options. The radius of the circle is 3 units. The center of the circle lies on the x-axis. The center of the circle lies on the y-axis. The standard form of the equation is (x – 1)² + y² = 3. The radius of this circle is the same as the radius of the circle whose equation is x² + y² = 9.

Answer 1

• The center of the circle lies on the x-axis
• The radius of the circle is 3 units.
• The radius of this circle is the same as the radius of the circle whose equation is x² + y² = 9.

The standard equation of a circle is expressed as:

`x^(2) +y^(2) +2gx+2fy+C=0`

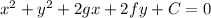
• Centre is (-g, -f)
• radius = √g²+f²-C
  

Given a circle whose equation is
`x^(2) +y^2-2x-8=0`.

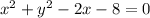Get the centre of the circle

2gx = -2x

2g = -2

g = -1

Similarly, 2fy = 0

f = 0

Centre = (-(-1), 0) = (1, 0)

This shows that the center of the circle lies on the x-axis

r = radius = √g²+f²-C

radius = √1²+0²-(-8)

radius =√9 = 3 units

The radius of the circle is 3 units.

For the circle x² + y² = 9, the radius is expressed as:

r² = 9

r = 3 units

Answer:

The radius of this circle is the same as the radius of the circle whose equation is x² + y² = 9.

Answer 2

The answer are

The centre of the circle lies on the x axis

The standard form of the equation is (x–1)²+y=3²

Explanation:

x²+y²-2x-8=0

x²-2x+y²=8

x²-2x+1+y²=8+1

(x-1)²+y²=9