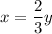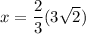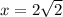Question

Find the values of X and Y when the smaller triangle has an area of 6cm2.

the value of X?
the value of Y?

Answer 1

• x = 2√2 cm
• y = 3√2 cm

Explanation:

You want to know the dimensions x and y of a smaller triangle with an area of 6 cm² if the larger similar triangle has corresponding dimensions 8 cm and 12 cm.

Scale factor

The scale factor between the dimensions is the square root of the scale factor between the areas.

scale factor = √((smaller area)/(larger area))

The larger area is given by the triangle area formula ...

A = 1/2bh

A = 1/2(12 cm)(8 cm) = 48 cm²

Using this value with the given area of the smaller triangle, we find the scale factor to be ...

scale factor = √((6 cm²)/(48 cm²)) = √(1/8) = √(2/16) = (√2)/4

Dimensions

Each of the smaller triangle dimensions is the product of this scale factor and the corresponding larger triangle dimension:

x = (8 cm)(√2)/4

x = 2√2 cm

and

y = (12 cm)(√2)/4

y = 3√2 cm

Answer 2

`y = 3\sqrt{2`

`x = 2\sqrt2`

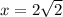
Explanation:

We are given that the triangles are similar, so the ratio of their side lengths is the same:

`(x)/(y) = (8)/(12)`

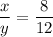
↓ simplifying the right fraction

`(x)/(y) = (2)/(3)`

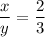
↓ multiplying by y to solve for x

`x = (2)/(3)y`

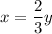
Now, we can create a system of equations by plugging x and y into the triangle area formula (using the given area of the smaller triangle):

`A =(1)/(2) bh`

`6 = (1)/(2) xy`

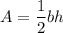
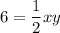
From here, we can substitute the x definition in terms of y into this equation to solve for y.

`\begin{cases} x = (2)/(3)y \\ \\ 6 = (1)/(2) xy\end{cases}`

`6 = (1)/(2) \left((2)/(3)y\right)y`

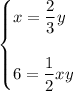
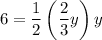
↓ simplifying the right side

`6 = (1)/(3)y^2`

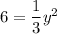
↓ multiplying by 3 on both sides

`18 = y^2`

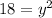
↓ taking the square root of both sides

`y = \sqrt{18`

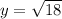
↓ simplifying the square root

`y=3\sqrt2`

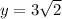
Finally, we can solve for x by plugging this y value into the first equation.

`x = (2)/(3)y`

`x = (2)/(3)(3√(2))`

`x = 2\sqrt2`