Question

NO LINKS!!! URGENT HELP PLEASE!!!

Solve ΔABC using the Law of Sines

1. A = 29°, C = 63°, c = 24

2. A = 72°, B= 35°, c = 21

Answer 1

1) B = 88°, a = 13.1, b = 26.9

2) C = 73°, a = 20.9, b = 12.6

Explanation:

To solve for the remaining sides and angles of the triangle, given two sides and an adjacent angle, use the Law of Sines formula:

`\boxed{\begin{minipage}{7.6 cm}\underline{Law of Sines} \\\\$(a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)$\\\\\\where:\\ \phantom{ww}$\bullet$ $A, B$ and $C$ are the angles. \\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides opposite the angles.\\\end{minipage}}`

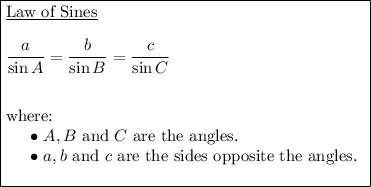
Question 1

Given values:

• A = 29°
• C = 63°
• c = 24

As the interior angles of a triangle sum to 180°:

`\implies A+B+C=180^(\circ)`

`\implies B=180^(\circ)-A-C`

`\implies B=180^(\circ)-29^(\circ)-63^(\circ)`

`\implies B=88^(\circ)`

Substitute the values of A, B, C and c into the Law of Sines formula and solve for sides a and b:

`\implies (a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)`

`\implies (a)/(\sin 29^(\circ))=(b)/(\sin 88^(\circ))=(24)/(\sin 63^(\circ))`

Solve for a:

`\implies (a)/(\sin 29^(\circ))=(24)/(\sin 63^(\circ))`

`\implies a=(24\sin 29^(\circ))/(\sin 63^(\circ))`

`\implies a=13.0876493...`

`\implies a=13.1`

Solve for b:

`\implies (b)/(\sin 88^(\circ))=(24)/(\sin 63^(\circ))`

`\implies b=(24\sin 88^(\circ))/(\sin 63^(\circ))`

`\implies b=26.9194211...`

`\implies b=26.9`

`\hrulefill`

Question 2

Given values:

• A = 72°
• B = 35°
• c = 21

As the interior angles of a triangle sum to 180°:

`\implies A+B+C=180^(\circ)`

`\implies C=180^(\circ)-A-B`

`\implies C=180^(\circ)-72^(\circ)-35^(\circ)`

`\implies C=73^(\circ)`

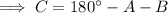
Substitute the values of A, B, C and c into the Law of Sines formula and solve for sides a and b:

`\implies (a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)`

`\implies (a)/(\sin 72^(\circ))=(b)/(\sin 35^(\circ))=(21)/(\sin 73^(\circ))`

Solve for a:

`\implies (a)/(\sin 72^(\circ))=(21)/(\sin 73^(\circ))`

`\implies a=(21\sin 72^(\circ))/(\sin 73^(\circ))`

`\implies a=20.8847511...`

`\implies a=20.9`

Solve for b:

`\implies (b)/(\sin 35^(\circ))=(21)/(\sin 73^(\circ))`

`\implies b=(21\sin 35^(\circ))/(\sin 73^(\circ))`

`\implies b=12.5954671...`

`\implies b=12.6`