Question

PLEASE HELPPPP I NEED THIS ITS OVER DUE!!!!!

Answer 1

3) tanθ = -√3

4) tanθ = undefined

Explanation:

For your third problem, we are given:

`\displaystyle{\cos \theta = -(1)/(2)}`

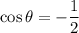
And
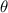`\displaystyle{\theta}` lies in quadrant 2 which is
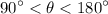`\displaystyle{90^(\circ) < \theta < 180^(\circ)}`. Since tangent is the division of sine over cosine, and cosine is in negative while sine is positive according to unit circle in quadrant 2. Therefore, the value of tangent is negative.

We lack sinθ to find tanθ. Therefore, we have to find sinθ first. We can use the identity:

`\displaystyle{\sin^2 \theta + \cos^2 \theta = 1}`

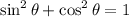
To solve for sinθ, subtract cos²θ both sides:

`\displaystyle{\sin^2 \theta + \cos^2 \theta - \cos^2 \theta= 1-\cos^2 \theta}\\\\\displaystyle{\sin^2 \theta= 1-\cos^2 \theta}`

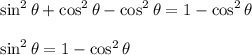
Substitute cosθ = -1/3. Therefore:

`\displaystyle{\sin^2 \theta= 1-\left(-(1)/(2)\right)^2}\\\\\displaystyle{\sin^2 \theta= 1-(1)/(4)}\\\\\displaystyle{\sin^2 \theta=(4)/(4)-(1)/(4)}\\\\\displaystyle{\sin^2 \theta = (3)/(4)}`

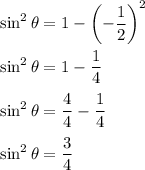
Since the value of sinθ is positive in quadrant 2. Hence:

`\displaystyle{\sin \theta = \sqrt{(3)/(4)}}\\\\\displaystyle{\sin \theta = (√(3))/(2)}}`

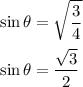
Now find the value of tanθ by sinθ/cosθ. Therefore:

`\displaystyle{\tan \theta = ((√(3))/(2))/(-(1)/(2))}\\\\\displaystyle{\tan \theta = -√(3)}`

Therefore, tanθ = -√3.

Next, to your fourth problem. To find tanθ again but given that sinθ = -1 in range of 0 ≤ θ < 2π.

Again, we have to apply the identity like the third problem. In this case, we solve for cosθ so we have the formula of:

`\displaystyle{\cos^2 \theta = 1-\sin^2 \theta}`

Substitute in sinθ:

`\displaystyle{\cos^2 \theta = 1-(-1)^2}\\\\\displaystyle{\cos^2 \theta = 1-1}\\\\\displaystyle{\cos^2 \theta = 0}`

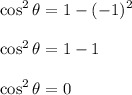
Therefore:

`\displaystyle{\cos \theta = 0}`

Since tanθ is sinθ/cosθ. We have -1/0 which is undefined. Therefore there are no tanθ values.