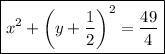Question

The diameter of Circle Q terminates on the circumference of the circle at (0,3)and (0,−4). Write the equation of the circle in standard form. Show all of your work.

Need answer ASAP Please!!

Answer 1

`x^2+\left(y+(1)/(2)\right)^2=(49)/(4)`

Explanation:

The center of the circle is the midpoint of its diameter.

`\boxed{\begin{minipage}{7.4 cm}\underline{Midpoint between two points}\\\\Midpoint $=\left((x_2+x_1)/(2),(y_2+y_1)/(2)\right)$\\\\\\where $(x_1,y_1)$ and $(x_2,y_2)$ are the endpoints.\\\end{minipage}}`

Given the endpoints of the diameter are (0, 3) and (0, -4), to find the coordinates of the center of the circle, substitute the two endpoints into the midpoint formula:

`\text{Center}=\left((0+0)/(2),(-4+3)/(2)\right)=\left(0,-(1)/(2)\right)`

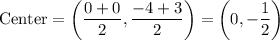
As the x-values of the endpoints of the diameter are the same, the length of the diameter, d, is the absolute value of the difference in y-values of the endpoints:

`d=|3-(-4)|=7`

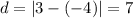
Therefore, the diameter of circle Q is 7 units.

The radius, r, of a circle is half its diameter. Therefore:

`r=(d)/(2)=(7)/(2)`

`\boxed{\begin{minipage}{4 cm}\underline{Equation of a circle}\\\\$(x-h)^2+(y-k)^2=r^2$\\\\where:\\ \phantom{ww}$\bullet$ $(h,k)$ is the center. \\ \phantom{ww}$\bullet$ $r$ is the radius.\\\end{minipage}}`

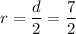
Now we have determined the center and radius of circle Q, we can substitute these values into the equation of a circle to write the equation of circle Q in standard form:

`(x-0)^2+\left(y-\left(-(1)/(2)\right)\right)^2=\left((7)/(2)\right)^2`

`x^2+\left(y+(1)/(2)\right)^2=(49)/(4)`

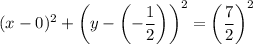
Therefore, the equation of circle Q in standard form is:

`\boxed{x^2+\left(y+(1)/(2)\right)^2=(49)/(4)}`