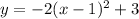Question

Write an equation (any form) for the quadratic graphed below

Answer 1

`y = -2(x - 1)^2 + 3`

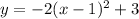
Explanation:

The given figure which is a quadratic is the shape of a parabola

The general vertex form equation of a parabola is

`y = a(x - h)^2 + k`

where,
( h, k ) is the vertex and a is a constant

Looking at the figure we see the vertex is at
`(1, 3)`

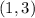
So the equation of the parabola is

`y = a(x - 1)^2 + 3`

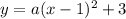
To compute the constant
`a` take a point (x, y) through which the parabola passes, plug in these x, y values into the above equation and solve

The parabola passes through point
`(3, -5)`

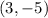
Plugging

`x = 3, y = -5`

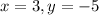
gives

`- 5 = a(3-1)^2 + 3\\\\-5 = a\cdot 2^2 + 3\\\\-5 = 4a + 3\\\\-5-3=4a\\\\-8 = 4a\\\\a = -8/4 = -2\\\\`

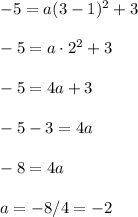
Therefore the equation of the given quadratic(parabola) is

`y = -2(x - 1)^2 + 3`