Question

The table represents a quadratic function f(x).

x f(x)
−4 7
−3 6
−2 7
−1 10
0 15
1 22
2 31

If the equation of the function f(x) is written in standard form f(x) = ax2 + bx + c, what is the value of b?
A) 3
B) 6
C) 16
D) 22

Answer 1

B) 6

Explanation:

Calculate the value of c by substituting point (0, 15) into the quadratic equation formula:

`f(x)=ax^2+bx+c`

`\begin{aligned}f(0)=a(0)^2+b(0)+c&=15\\0+0+c&=15\\c&=15\end{aligned}`

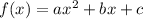
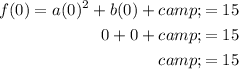
Therefore:

`f(x)=ax^2+bx+15`

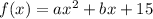
Substitute the point (1, 22) into the formula and create an equation for a in terms of b:

`\begin{aligned}f(1)=a(1)^2+b(1)+15&=22\\a+b+15&=22\\a+b&=7\\a&=7-b\end{aligned}`

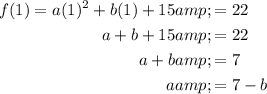
Therefore:

`f(x)=(7-b)x^2+bx+15`

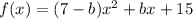
Finally, substitute another point from the table (-3, 6) and solve for b:

`\begin{aligned}f(-3)=(7-b)(-3)^2+b(-3)+15&=6\\(7-b)9-3b+15&=6\\63-9b-3b+15&=6\\78-12b&=6\\-12b&=-72\\b&=6\end{aligned}`

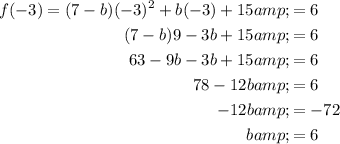
Therefore, the value of b is 6.