Question

Write two different quadratic functions that go through the points (5,3) and (8,0). (PLEASE ANSWER CORRECTLY)

Answer 1

`y=x^(2) -14x+48` (when a=1)

`y=2x^(2) -27x+88` (when a=2)

The general form of the quadratic functions you asked is :

`y=a(x-5)(x-8)-x+8\\(a\\eq 0)`

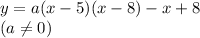
Here,

-x+8 is a line that passes two given points.

When you put x=5, you get y=3,

which is a coordinate of one of the given points.

When you put x=8, you get y=0,

which is a coordinate of the other one.

-----------------------------------------------------------------------------------------------------

This is the way I got the form above :

Since what we're looking for is a quadratic function, (let's call it "f(x)")

the equation

f(x)=-x+8

can have at most 2 different real solutions.

You can note that the real solution of the equation above

represents the x coordinate of the intersection point of two graphs:

y=f(x) and y=-x+8.

Again, the equation can have at most 2 different solutions.

And we have 2 different real solutions already given -

(It's a requirement ; we want y=f(x) to contain (5,3) and (8,0))

- which are x=5, x=8.

So these are the only two solutions of the equation.

Since the coefficient of a highest order term

hasn't been decided, we can introduce an unknown 'a' for it.

(i.e. Let 'a' be the coefficient of a highest order term.)

To sum up, an equation

f(x)=-x+8

f(x)+x-8=0

has two different real solutions x=5, x=8,

thus it can be written like this;

a(x-5)(x-8)=0

where a is not zero.

Therefore

f(x)+x-8 = a(x-5)(x-8)

(Because two italic-texted equations have the same meaning)

∴
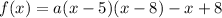
`f(x)=a(x-5)(x-8)-x+8`
`\QED`.