Question

1. The data sel below represents the number of animals in different exhibits at a zoo.

48, 86, 15, 27, 18, 52, 103
a. Write the data from least to greatest.
h. What is the minimum number of animals?
c. What is the maximum number of animals?
d. What is the median number of animals?
e. What is the median of the first half of the data? (first quartile)
f. What is the median of the second half of the data? (third quartile)
g. What is the interquartile range?

Answer 1

a) 15, 18, 27, 48, 52, 86, 103

b) Minimum number = 15

c) Maximum number = 103

d) Median = 48

e) First quartile = 18

f) Third quartile = 86

g) Interquartile range = 68

Explanation:

Part a

To write the data from least to greatest, arrange the numbers in ascending order:

• 15, 18, 27, 48, 52, 86, 103

`\hrulefill`

Part b

The minimum number in a set of data is the smallest value.

Therefore, the minimum number of animals is 15.

`\hrulefill`

Part c

The maximum number in a set of data is the greatest value.

Therefore, the maximum number of animals is 103.

`\hrulefill`

Part d

The median of a set of data is the middle value when all data values are placed in order of size.

`\begin{array}{ccccccc}\sf 15, &\sf 18, &\sf 27, &\sf 48, &\sf 52, &\sf 86,& \sf 103\\ &&&\uparrow&&&\\&&&\sf median&&&\end{array}`

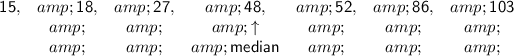
Therefore, the median is the fourth number, which is 48.

`\hrulefill`

Part e

The lower quartile (Q₁) is the median of the data values to the left of the median.

`\begin{array}{ccccccc}\sf 15, &\sf 18, &\sf 27, &\sf 48, &\sf 52, &\sf 86,& \sf 103\\ &\uparrow &&\uparrow&&&\\&\sf Q_1&&\sf median&&&\end{array}`

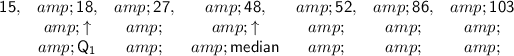
Therefore, the median of the first half of the data is 18.

`\hrulefill`

Part f

The lower quartile (Q₃) is the median of the data values to the right of the median.

`\begin{array}{ccccccc}\sf 15, &\sf 18, &\sf 27, &\sf 48, &\sf 52, &\sf 86,& \sf 103\\ &&&\uparrow &&\uparrow&\\&&&\sf median&&\sf Q_3&\end{array}`

Therefore, the median of the second half of the data is 86.

`\hrulefill`

Part g

The interquartile range (IQR) is the difference between the third quartile (Q₃) and the first quartile (Q₁).

`\begin{aligned}\sf IQR &=\sf Q_3 - Q_1 \\&= \sf 86 - 18 \\&= \sf 68\end{aligned}`

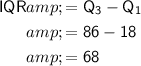
Therefore, the interquartile range is 68.