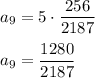Question

15,10,20/3,... find the 9th term

Answer 1

9th term is

`a_9 = (1280)/(2187)\\`

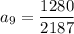
Explanation:

This sequence is clearly a geometric progression where the ratio of any term to the previous term is constant and known as common ratio

The 3 terms given are:
15, 10 and 20/3

10 ÷ 15 = 2/3

20/3 ÷ 10 = 2/3

So the common ratio is 2/3

For a geometric sequence with common ratio r and first term a₁, the nth term is given by the equation

aₙ = a₁ · rⁿ⁻¹

Here a₁ = first term = 15

r = 2/3

So the general equation for the nth term of this equation is
aₙ = 15 · (2/3)ⁿ⁻¹

The 9th term would be

`a_9 = 15 \cdot \left((2)/(3)\right)^(9-1)\\\\a_9 = 15 \cdot \left((2)/(3)\right)^(8)\\\\a_9 = 15 \cdot \left((256)/(6561)\right)\\\\a_9 = 15 \cdot \left((256)/(6561)\right)\\`
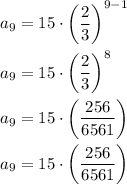
15 is divisible by 3 giving 5
6561 is divisible by 3 giving 2187

So the above expression simplifies to

`a_9 = 5 \cdot (256)/(2187)\\\\a_9 = (1280)/(2187)\\`