Question

Solve the equation 3x+4/3 - 2x/x-3 =x

Answer 1

x = -6.

Explanation:

1. Write the equation.

`\sf (3x+4)/(3) -(2x)/(x-3) =x`

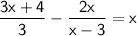
2. Multiply by "3" on both sides ob the equation.

Applying the distributive property of multiplication on the left hand side:

`\sf (3)((3x+4)/(3) -(2x)/(x-3)) =x(3)\\ \\ \\{3x+4} -((3)2x)/(x-3)=3x\\ \\ \\{3x+4} -(6x)/(x-3)=3x`

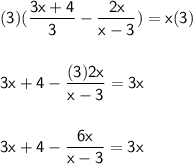
3. Multiply by "x-3" on both sides ob the equation.

Applying the distributive property of multiplication:

`\sf (x-3)({3x+4} -(6x)/(x-3))=3x(x-3)\\ \\ \\(x-3)({3x+4}) -6x=3x(x-3)\\ \\ \\(x)(3x)+(x)(4)+(-3)(3x)+(-3)(4) -[6x]=3x(x-3)\\ \\ \\`

Check the image below to see an illustration of this process.

`\sf 3x^(2) +4x-9x-12 -[6x]=3x(x-3)\\ \\ \\3x^(2) +4x-9x-12 -6x=3x(x-3)\\ \\ \\3x^(2) -11x-12 =3x(x-3)`

Now simplifying on the right hand side (applying the same logic as last step).

`\sf 3x^(2) -11x-12 =3x(x-3)\\ \\ \\3x^(2) -11x-12 =(3x)(x)+(3x)(-3)\\ \\ \\3x^(2) -11x-12 =3x^(2)-9x`

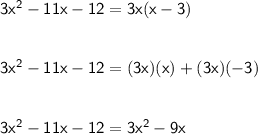
4. Add "9x" on both sides of the equation.

`\sf 3x^(2) -11x-12+9x =3x^(2)-9x+9x\\ \\ \\3x^(2) -2x-12 =3x^(2)`

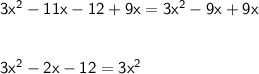
5. Subtract "3x²" from both sides.

`\sf 3x^(2) -2x-12-3x^(2) =3x^(2)-3x^(2)\\ \\ \\-2x-12 =0`

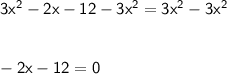
6. Add "12" on both sides.

`\sf -2x-12+12=0+12\\ \\ \\-2x=12`

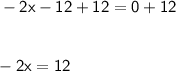
7. Divide by "-2" ob both sides.

`\sf (-2x)/(-2) =(12)/(-2) \\ \\ \\x =-6`

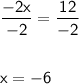
8. Verify the answer.

If "x= -6" is the correct answer, substituting "x" by "-6" on the original equation should return the same value on both sides of the equal (=) symbol. Let's test!

`\sf (3(-6)+4)/(3) -(2(-6))/((-6)-3) =(-6)\\ \\-6=-6`

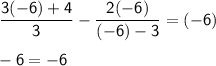
That's correct!

x = -6 is the corect answer.