Question

PLEASE HELP ME QUICK!!!

Answer 1

Option D.
`g(x)=5(0.8)^(x)+2`

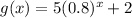
Explanation:

Main concepts

Concept 1: identifying horizontal asymptote

Concept 2: assuring decreasing exponential function

Concept 1. identifying horizontal asymptote

Any exponential function of the form
`y=a*b^x` has a horizontal asymptote on the x-axis. A constant (positive or negative) added to the end of the exponential expression will shift the graph of the exponential function up (if positive) or down (if negative) the number of units equal to the magnitude of the number. Since the original function f(x) has a "+2" at the end, it has been shifted up 2 units. Thus, we can eliminate answers A and C from feasible answers since they each shift the exponential function up 3 units, not 2.

Concept 2. assuring decreasing exponential function

Exponential functions of the form
`y=a*b^x` increase or decrease based on the value of "b".

• If "b" is between 0 and 1 (a "small" number), the function will decrease.
• If "b" is larger than 1 (a "big" number), the function will increase.

Observe that the graph of the function f(x) is decreasing, and the value of b=0.5.

To ensure that g(x) also decreases, the b-value must be between 0 and 1, which eliminates option B.

Option D is the correct answer because the value of "b" is between 0 and 1 (making the graph of the function a decreasing exponential), and the number added at the end is "+2", causing the horizontal asymptote to be at a height of positive 2.